Binary number
Binary numbering system uses only two symbols 0 and 1. Each digits of a binary number is referred to as bits. Binary system is also known as base -2 system. Each digit is represented by the increasing power of 2 from the LSB (Least Significant Bit). Binary system is the heart of digital electronics and is used for information flow. In digital electronics, 0 and 1 are used to denote logic states, high and low. Arithmetic operations are also possible in binary system.
Gray code
Gray code, also known as reflected binary code, is a code having digits 0 and 1. Gray code do not have place value for its digits. Any successive codes in Gray code system have only one bit changes.
Gray code to binary conversion can be made easy with an example:
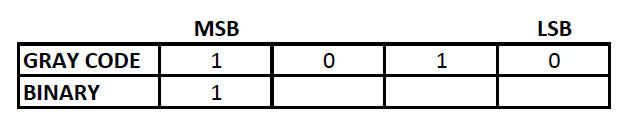
Let us convert 1010 from gray code to binary value:
Step 1: The MSB (Most Significant Bit) of a binary and gray code will be the same.
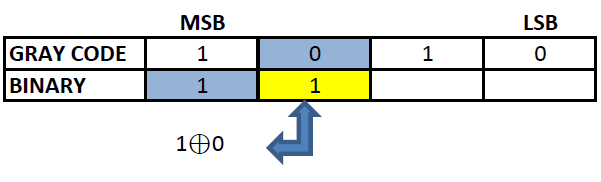
Step 2: The next digit of binary will be the EXOR of the MSB of binary and the second MSB of the gray code.
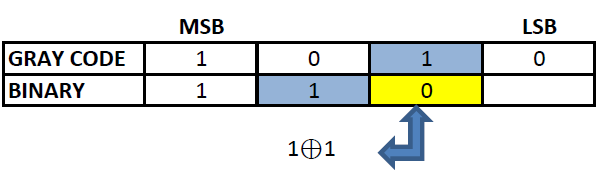
Step 3: Similarly EXOR the digit obtained in the previous step and the third MSB of gray code to obtain the third MSB of binary.
Step 4: Repeat the previous step till the LSB of gray code is found.
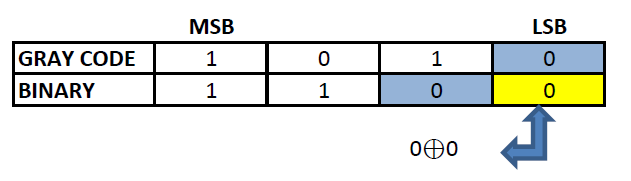
Binary corresponding to gray code 1010 is 1100.
Use Gray to Binary convertor
Gray to Binary Conversion table
| Decimal | Gray | Binary |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0011 | 0010 |
| 3 | 0010 | 0011 |
| 4 | 0110 | 0100 |
| 5 | 0111 | 0101 |
| 6 | 0101 | 0110 |
| 7 | 0100 | 0111 |
| 8 | 1000 | 1100 |
| 9 | 1101 | 1001 |
| 10 | 1111 | 1010 |
| 11 | 1110 | 1011 |
| 12 | 1010 | 1100 |
| 13 | 1011 | 1101 |
| 14 | 1001 | 1110 |
| 15 | 1000 | 1111 |